Importância da Física
A Física é a base de toda a Engenharia e Tecnologia
Cientistas de todas as áreas usam os conceitos da Física: paleontologia, biologia, climatologia, medicina, etc.
A Física busca explicar o universo observável (e não tão observável…)
A Física é uma conquista da raça humana (que começou com Tales…)
Tanto quanto se sabe, Tales, filósofo grego, da cidade de Mileto, foi o primeiro a tentar entender qual a origem do universo.
Diferente de seus contemporâneos, acreditava que as coisas tinham uma explicação natural, e não mística.
Tales de Mileto, 624-556 AC
A Física é uma ciência experimental
A “matéria prima” da Física são os fenômenos. Fenômenos são observados na busca de padrões. Para estes padrões tenta-se estabelecer uma ‘explicação’.
Fenômenos: na Física, significa o mundo como nós o experimentamos, isto é, os fatos como são percebidos por nossos sentidos. Por exemplo, o movimento dos corpos celestes, a queda dos corpos, o movimento das marés, a força exercida pelo vento.
Padrões: tenta-se detectar um padrão de repetição nos fenômenos, ou uma relação causa-efeito. Por exemplo, próximos ao Sol, os planetas movem-se mais rápido, a velocidade da queda não depende da massa, as marés estão relacionadas à Lua, a força captada do vento depende da área, etc.
“Explicação”:com base em observação, experimentos e repetições, estabelece-se uma explicação, ou lei, matemática para o fenômeno. Isso permitirá que a lei seja aplicada a fenômenos semelhantes (por exemplo, uma ponte de palitos, ou uma ponte ‘de verdade’), ou permitirá prever o que ocorrerá no futuro, como quando uma nave é enviada a outro planeta.
A importância dos modelos
Os fenômenos, em geral, são bastante complexos. Para estudá-los constroem-se modelos. Um modelo é uma construção que simplifica o fenômeno observado, isolando as características e variáveis que se deseja estudar.
Galileu Galilei, que pode ser considerado o ‘pai’ da Física Moderna, foi um dos primeiros a utilizar esse método. Ao observar um fenômeno, ele construía um modelo, realizava experimentos, e buscava estabelecer uma lei matemática com base neles.
Por exemplo, foi assim com o movimento pendular, a partir da observação do candelabro da Catedral de Pisa, sua cidade.
Grandezas e Unidades
Uma vez que as leis da Física devem ser matemáticas, é necessário atribuir números aos elementos de um fenômeno, isto é, quantificá-los. Assim, definimos:
Grandeza física: é a característica que queremos medir. Alguns exemplos: massa, velocidade, tempo, tensão, resistência elétrica, etc. As grandezas podem ser:
Escalares: se precisarem apenas de um número. Por exemplo: massa, temperatura, pressão.
Vetoriais: se precisarem também da indicação da direção e do sentido. Por exemplo: força, velocidade
Unidade: é a escala usada para medir a grandeza. Há uma variedade de unidades para a mesma grandeza. Por exemplo, podemos medir uma distância em metros, jardas, milhas, braças.
Sistema Internacional de Unidades
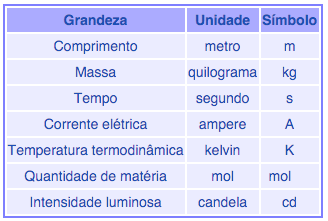
Para uniformidade, desde o final do século XIX, buscou-se estabelecer um sistema de unidades comuns a todos os pesquisadores, e hoje, praticamente todos os países o adotam com o nome de Sistema Internacional de Unidades. No Brasil, a entidade responsável por suas definições é o INMETRO, e a descrição completa do SI pode ser encontrada em: http://www.inmetro.gov.br/noticias/conteudo/sistema-internacional-unidades.pdf. Algumas definições fundamentais são:
Incerteza e algarismos significativos
Nos experimentos e nos cálculos na Física e na Engenharia lidamos com muitas medidas. As medidas sempre envolvem um nível de incerteza, e por isso é importante indicá-las corretamente. Por exemplo, se usarmos uma régua milimétrica para medir o diâmetro de uma peça redonda, não seria correto indicar o resultado como 15,0 mm, pois a régua não mede décimos de milímetros. A indicação correta, seria 15 mm. Se a mesma peça tivesse sido medida com um paquímetro, porém, poderíamos indicar 15,2 mm, já que o paquímetro tem uma precisão de 0,1 mm. Igualmente, se fizermos essa medição com um micrômetro, poderíamos indicar 15,23 mm, pois o micrômetro nos dá uma leitura centesimal das medidas.
A diferença entre essas indicações é a incerteza. A medição do micrômetro tem uma incerteza menor - ela é mais precisa. Por isso não podemos indicar 15,00 mm para a medida com a escala. Observe as diferenças entre os 3 instrumentos:
Escala Paquímetro Micrômetro
Podemos indicar o erro provável de uma medição escrevendo o número seguido do símbolo +/- e daí o erro. Por exemplo:
significa que a medida “d” estará entre 15,5 e 15,9 mm.
Pode ser também feita uma indicação percentual.
Uma notação usada por alguns autores é:
onde o número entre parênteses indica a possível variação do último algarismo do valor da grandeza, resultando, igualmente, em 15,7 a 15,9 mm.
Nos casos em que a incerteza não é explicitada usando as formas acima, ela é indicada pelo número de algarismos significativos usados, no qual o último dígito indicará uma incerteza unitária. Por exemplo, quando indicamos:
estamos fornecendo 3 algarismos significativos e informando que a incerteza está no último (0,2), com um erro de aproximadamente +/- 0,1 mm. Essa seria uma indicação correta para um paquímetro com precisão de 0,1 mm, por exemplo.
Se indicamos
também estamos fornecendo 3 algarismos significativos, e estamos informando que o erro deverá ser de 1 km, ou seja, a distância estará entre 252 e 254 km.
Algarismos significativos nos cálculos
Quando operamos cálculos com vários graus de incerteza, a resposta deve ser consistente com os dados que temos.
Soma
Na soma, por exemplo, suponha que vamos adicionar um comprimento de 14,75 com um de 8,1. O resultado final deverá indicar o nível de incerteza do dado com o menor nível incerteza. Assim:
O resultado matemático seria 22,82, que, porém, está incorreto do ponto de vista físico, pois indicaria um nível de incerteza irreal.
Multiplicação
Na multiplicação, o resultado final deverá ter o mesmo número de algarismos significativos do dado com o menor número de algarismos significativos. Por exemplo:
Repare que a resposta matemática seria 4,26377952, que, porém, não tem sentido físico, pois não temos precisão suficiente para afirmar que este é o valor correto. De todos os algarismos que participam do produto, o que tem menos algarismos significativos tem 2 (0,58). Assim, a resposta correta deve indicar apenas 2 algarismos significativos.
Para manter a indicação das medidas consistentes, é conveniente usar a notação de potência de 10. Assim, a indicação da distância à Lua como 384.000.000 m não estaria correta, pois indica um nível de incerteza que com toda probabilidade não reflete a realidade. O mais coerente seria indicar:
Essa seria uma indicação com 3 algarismos significativos, em que a incerteza recai na casa dos milhões de metros, e não do metro.
Se tivermos um valor mais preciso, podemos indicar concordemente. Por exemplo, o site da NASA dá as seguintes informações sobre a Lua:

Observe que tanto a indicação decimal como a científica estão coerentemente fornecidas com o mesmo número de algarismos significativos
Certos valores que aparecem nas formas são uma exceção. Por exemplo:
Tanto o 2 do expoente como o 2 do denominador são tomados como valores exatos.
Por exemplo:
A energia de repouso E de um corpo de massa m é dada pela equação de Einstein:
onde c é a velocidade da luz no vácuo, cujo valor é 299.792.458 m/s. Determine E para a massa do elétron, dada como:
Fazendo as substituições, teremos:
Como vimos, porém, o resultado deverá ser indicado com o mesmo número de algarismos significativos do dado com o menor número deles, neste caso 3 (9,11 x 10-31):
Arrendondamento
Para as regras de arredondamento, a norma ABNT-NBR 5891:2014 estabelece o seguinte:
- Quanto o algarismo a ser conservado for seguido de um algarismo inferior a 5, permanece o algarismo conservado e retiram-se os posteriores. Exemplos:
1,439 arredondado para uma casa depois da vírgula ficará 1,4
3,14159 arredondado para duas casas depois da vírgula ficará 3,14
- Quando o algarismo a ser conservado for seguido de um número superior a 5, ou de um número igual a 5 seguido de no mínimo um algarismo diferente de zero, soma-se uma unidade ao algarismo a ser conservado e elimina-se o resto. Exemplos:
4,368 arredondado para uma casa depois da vírgula ficará 4,4
13,75000001 arredondado para uma casa depois da vírgula ficará 13,8
- Quando o número subsequente ao que queremos arrendondar for igual a 5 e posteriormente zero, se o algarismo a ser conservado for par, ele ficará par; se for ímpar, será acrescido de uma unidade. Exemplos:
3,25 arredondado para uma casa depois da vírgula ficará 3,2
3,75 arredondado para uma casa depois da vírgula ficará 3,8
Próximos passos
Sessão de Introdução à Física Elétrica
Filme sobre a História da Eletricidade