Name: 
 

Função quadrática, raízes


Escolha a alternativa correta
 

1. 
A soma e o produto das raízes da equação 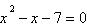quad_raizes_files/i0020000.jpg são, nessa ordem, iguais a:
a.
1, -7
b.
-1, -7
c.
1, 7
d.
-1, -7
e.
-7, 1
 

2. 
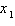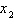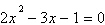Considere as proposições a seguir em que quad_raizes_files/i0030000.jpg e quad_raizes_files/i0030001.jpg são as raízes de quad_raizes_files/i0030002.jpg.
quad_raizes_files/i0030003.jpg
O número de proposições verdadeiras é:
a.
0
b.
1
c.
2
d.
3
e.
4
 

3. 
Sobe a equação 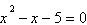quad_raizes_files/i0040000.jpg, considere as 4 afirmações a seguir:
I. O inverso da soma das suas raízes é 1.
II. A soma dos inversos de suas raízes é 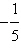quad_raizes_files/i0040001.jpg
III. O quadrado da soma das suas raízes é 1.
IV. A soma do quadrado de suas raízes é 11.
O número de afirmações corretas é:
a.
0
b.
1
c.
2
d.
3
e.
4
 

4. 
A forma fatorada de 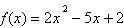quad_raizes_files/i0050000.jpg é:
a.
quad_raizes_files/i0050001.jpg
b.
quad_raizes_files/i0050002.jpg
c.
quad_raizes_files/i0050003.jpg
d.
quad_raizes_files/i0050004.jpg
e.
quad_raizes_files/i0050005.jpg
 

5. 
Com quad_raizes_files/i0060000.jpg e quad_raizes_files/i0060001.jpg, quad_raizes_files/i0060002.jpg é igual a:
a.
quad_raizes_files/i0060003.jpg
b.
quad_raizes_files/i0060004.jpg
c.
quad_raizes_files/i0060005.jpg
d.
quad_raizes_files/i0060006.jpg
e.
quad_raizes_files/i0060007.jpg
 

6. 
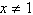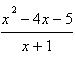Com quad_raizes_files/i0070000.jpg, quad_raizes_files/i0070001.jpg é igual a:
a.
quad_raizes_files/i0070002.jpg
b.
quad_raizes_files/i0070003.jpg
c.
quad_raizes_files/i0070004.jpg
d.
quad_raizes_files/i0070005.jpg
e.
quad_raizes_files/i0070006.jpg
 

7. 
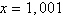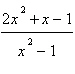Se quad_raizes_files/i0080000.jpg, então quad_raizes_files/i0080001.jpg é igual a:
a.
1000
b.
1001
c.
1002
d.
1004
e.
1008
 

8. 
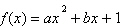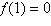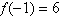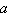(EEAR 2019) Seja a função quadrática quad_raizes_files/i0090000.jpg. Se quad_raizes_files/i0090001.jpg e quad_raizes_files/i0090002.jpg, então o valor de quad_raizes_files/i0090003.jpg é:
a.
5
b.
4
c.
3
d.
2
e.
1
 

9. 
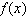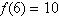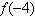(IFCE 2019) A função quadrática quad_raizes_files/i0100000.jpg tem gráfico com vértice de abscissa igual a 1. Sabendo que quad_raizes_files/i0100001.jpg, é correto afirmar-se que o valor de quad_raizes_files/i0100002.jpg é:
a.
15
b.
12
c.
-10
d.
10
e.
6
 

10. 
(EFOMM 2019) Examinte a função 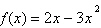quad_raizes_files/i0110000.jpg quanto à existência de valores máximos e mínimos. Assinale a alternativa correta:
a.
A função atinge o valor máximo de quad_raizes_files/i0110001.jpg para quad_raizes_files/i0110002.jpg
b.
A função atinge o valor mínimo de quad_raizes_files/i0110003.jpg para quad_raizes_files/i0110004.jpg
c.
A função atinge o valor máximo de quad_raizes_files/i0110005.jpg para quad_raizes_files/i0110006.jpg
d.
A função atinge o valor mínimo de quad_raizes_files/i0110007.jpg para quad_raizes_files/i0110008.jpg
e.
A função atinge o valor máximo de quad_raizes_files/i0110009.jpg para quad_raizes_files/i0110010.jpg
 

11. 
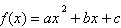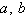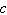(UEG 2019) As raízes de uma função quadrática quad_raizes_files/i0120000.jpg são -1 e 3. Sabendo-se que o vértice é o ponto (1, -4), os valores de quad_raizes_files/i0120001.jpg e quad_raizes_files/i0120002.jpg, são, respectivamente:
a.
-1, -2, -3
b.
1, -2, -3
c.
-1, 2, 3
d.
1, 2, 3
e.
-1, -2, 3
 

12. 
(EFOMM 2019) Considere a função 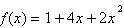quad_raizes_files/i0130000.jpg. Determine o valor da abscissa que define seu valor mínimo.
a.
-2
b.
-1
c.
quad_raizes_files/i0130001.jpg
d.
0
e.
1
 

13. 
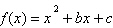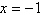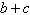(UECE 2019) Seja a função quadrática definida por quad_raizes_files/i0140000.jpg. Se seu valor mínimo ocorre para quad_raizes_files/i0140001.jpg e se 2 ´uma das raízes da equação, então, a soma quad_raizes_files/i0140002.jpg é igual a:
a.
-4
b.
4
c.
-6
d.
-3
e.
-2
 

14. 
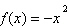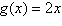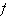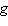(UEG 2018) Dadas as funções quad_raizes_files/i0150000.jpg e quad_raizes_files/i0150001.jpg, um dos pontos de interseção entre as funções quad_raizes_files/i0150002.jpg e quad_raizes_files/i0150003.jpg é:
a.
(0, 2)
b.
(-2, -4)
c.
(2, 4)
d.
(0, -2)
e.
(-2, 4)
 

15. 
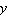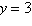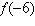(ESPM 2018, adaptada) Uma função quadrática tem como vértice o ponto (1, 2), e corta o eixo quad_raizes_files/i0160000.jpg em quad_raizes_files/i0160001.jpg. O valor de quad_raizes_files/i0160002.jpg é:
a.
74
b.
63
c.
42
d.
51
e.
37
 

16. 
(UDESC 2018) A função quadrática que contém os pontos (0, -9), (1, 0) e (2, 15) tem vértice em:
a.
(-2, 13)
b.
(1, 0)
c.
(0, -9)
d.
(2, 15)
e.
(-1, -12)
 

17. 
(UFJF 2017) É correto afirmar sobre a função quadrática 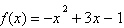quad_raizes_files/i0180000.jpg que:
a.
Ela é decrescente para 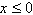quad_raizes_files/i0180001.jpg
b.
A concavidade é para cima
c.
Possui 3 raízes reais
d.
Seu vértice é 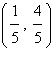quad_raizes_files/i0180002.jpg
e.
Seu valor máximo é 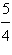quad_raizes_files/i0180003.jpg
 



 
Check Your Work     Reset Help