Definições
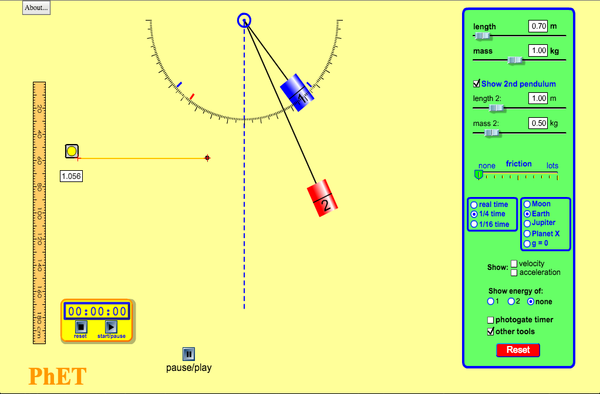
Dizemos que um fenômeno é periódico se ele repete-se em intervalos de tempos sucessivos e iguais. Abaixo estão dois exemplos simples de elementos mecânicos efetuando um Movimento Harmônico Simples. Repare que nos dois casos, há uma posição chamada de posição de equilíbrio, a partir da qual se verifica o movimento simétrico, para lados opostos, igual em módulo.
Nos dois casos também ocorre a presença de uma força restauradora, que tende a manter a massa na posição de equilíbrio: a força da gravidade no caso do pêndulo, e a elasticidade, no caso da mola.

Um pêndulo
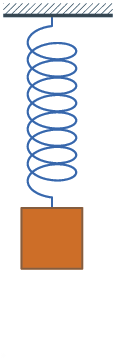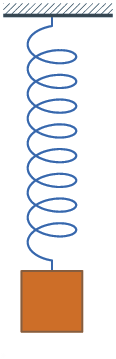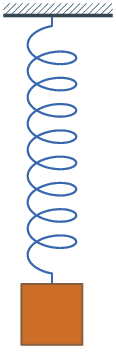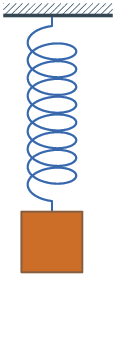
Um conjunto massa-mola
Relação entre o MHS e o Movimento Circular Uniforme (MCU)
Lembramos que o MCU, visto anteriormente, descreve o percurso de um ponto em uma trajetória circular, a uma velocidade constante. Quando comparamos o MHS com o MCU, verificamos que existe uma relação entre eles. Na figura abaixo, a massa da mola, em MHS, comporta-se como uma projeção do ponto que se move em MCU:
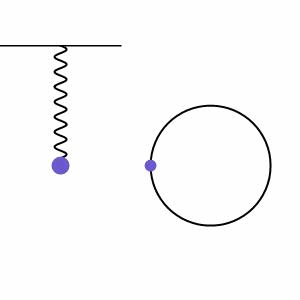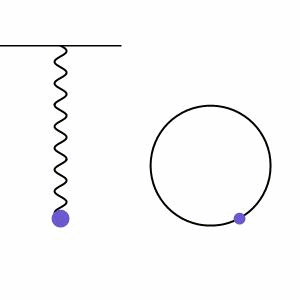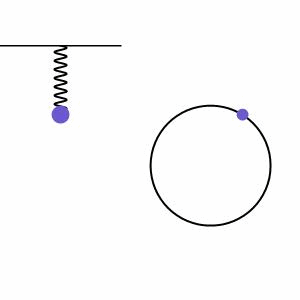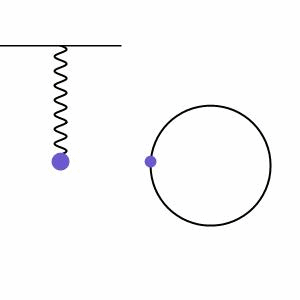
Por conta dessa relação, algumas definições do MCU aparecem também no MHS. São elas:
Ciclo: cada uma das repetições; no caso de um pêndulo, por exemplo, um movimento completo de vai-e-vem
Período (T): tempo de cada repetição ou ciclo. É medido em segundos, no SI.
Frequência (f): número de repetições por período. É medido em ciclos por segundo, ou Hertz (Hz) no SI.
O produto entre o período e frequência será sempre igual a um. Por exemplo, se um ponto oscila 10 vezes por segundo (frequência), quer dizer que ele leva 1/10 segundos para completar um ciclo (período). Portanto, 10 x 1/10=1. Assim, escrevemos:
No caso do MHS, uma medida importante também é a Amplitude. Ela é simplesmente a distância, em módulo, que vai do ponto de equilíbrio ao ponto de máximo afastamento. No exemplo abaixo, vemos que a mola, a partir do repouso, deslocou-se 20 centímetros abaixo, e 20 centímetros acima do ponto de repouso. Assim, a amplitude A do movimento foi de 20 cm, ou, no SI, 0,2 m.
No MHS também lidamos com ângulos, e muitas vezes são expresso em radianos. Para lembrar, um radiano corresponde à abertura angular cujo arco tem o mesmo comprimento do raio da circunferência no qual ele está inscrito
Se um ponto realiza um deslocamento “s” qualquer na trajetória circular, podemos calcular qual foi o deslocamento angular correspondente fazendo
Para fazer a transformação de radianos para graus, basta lembrar que o deslocamento total s, quando ele dá uma volta completa no círculo, é igual ao perímetro do círculo:
Como
Podemos fazer:
Ou seja, a volta completa tem 2π radianos. Como sabemos que uma volta completa tem também 360˚, podemos dizer que:
etc
Para realizar a conversão de qualquer valor, pode-ser fazer uma regra de três. Por exemplo, encontrar o valor em radianos correspondente a 30˚.
Outro exemplo: um ponto se descola 2,57 radianos. Qual seu deslocamento em graus?
OBS: O trabalho de redação em html continua… A seguir a aula e listas em pdf.
Simulador