O que acontece quando um corpo é deixado resfriar expontaneamente em um ambiente cuja temperatura possa ser considerada constante?
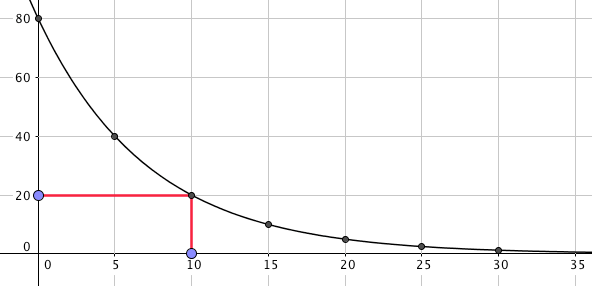
Se observarmos o resfriamento de um certo volume de água a 80˚C em um ambiente a 0˚C, por exemplo, notaremos um comportamento mostrado na tabela e no gráfico a seguir:
Newton estabeleceu que o resfriamento obedece à seguinte equação:
Ou seja, a taxa de variação da tempetura do esfriamento, ou a velocidade do esfriamento (em ˚C/s ou K/s, por exemplo) é diretamente proporcional a uma constante de proporcionalidade e à diferença de temperatura entre o corpo e o meio ambiente.
Assim, se não houver diferença de temperatura, a velocidade será zero.
Dedução da fórmula do esfriamento
Essa é uma equação diferencial ordinária de primeira ordem (EDO), e podemos resolvê-la pelo agrupamento de variáveis:
Integrando ambos os lados, teremos:
Da propriedade fundamental dos logaritmos, temos que:
![]()
Aplicando acima, podemos fazer:
Como a temperatura do corpo será sempre maior que a do ambiente, o logaritmando será sempre positivo, e o sinal de módulo é desnecessário.
Desenvolvendo:
Como eC é uma constante, a equação final fica:
Aplicação
Usando essa fórmula com a tabela acima, inicialmente calculamos o valor de C, pois temos que Ta=0˚C e para t=0 min, T=80˚C.
Assim, para o caso acima, temos que:
Para descobrir o valor de k, usamos a segunda informação, junto com a propriedade fundamental dos logaritmos: para t=5 min, T=40˚C.
Usando novamente a propriedade fundamental dos logaritmos:
Assim, a equação que descreve o comportamento acima é:
Por exemplo, qual será a temperatura desse corpo depois de um tempo de esfriamento de 10 min?
De fato: