Centro de massa de um corpo

No estudo dos movimentos, temos considerado os corpos como pontos, como se toda sua massa estivesse concentrada numa única região. Esse ponto, no qual podemos imaginar que a massa está concentrada, é chamado de centro de massa.
Por exemplo, sabemos que um corpo em movimento balístico se desloca de acordo com uma parábola. Repare que, no caso de um salto de um trampolim, que é um movimento dessa natureza, o movimento do centro de massa do corpo da mergulhadora descreve exatamente essa curva, embora o corpo do mergulhador possa realizar outros movimentos. Este filme do MIT mostra experiências semelhantes.
Um termo relacionado a centro de massa é centro de gravidade. A diferença entre eles é que o centro de massa não depende da ação gravitacional - é uma propriedade inerente do corpo. Se este corpo estiver sujeito a um campo gravitacional homogêneo, o centro de massa coincidirá com o centro de gravidade. Esse é o caso na maior parte das situações da Engenharia, e por isso, muitas vezes esses termos são usados como sinônimos, assim como o termo baricentro. A diferença entre o centro de massa e o centro de gravidade é importante em astrofísica e no comportamento dos satélites, por exemplo. Um outro termo desse contexto é centroide. O centroide de um corpo representa seu centro geométrico. Em outras palavras, ao passo que o centro de massa se refere à distribuição das massas, o centroide se refere à distribuição dos volumes.
Uma outra forma de pensar o centro de massa é imaginá-lo como o ponto pelo qual, se suspendermos o corpo, este não irá girar em nenhuma direção. Se tentarmos erguer um corpo por um ponto não alinhado verticalmente com o centro de massa, o corpo irá girar até que o ponto de içamento se alinhe com o centro de massa.
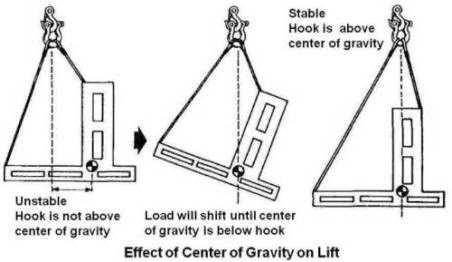
Fonte: http://practicalmaintenance.net/?p=748
Centro de massa de um grupo de corpos
Nos corpos sólidos regulares e homogêneos, como uma esfera um cubo ou um paralelogramo:
Um sistema composto por vários corpos também tem um centro de massa. As coordenadas do centro de massa do conjunto de corpos será dado pela média ponderada dos centros de massa de cada corpo, onde o fator de ponderação será a massa de cada corpo que compõe o sistema.
![]()
![]()
Por exemplo, dado o conjunto de 3 corpos abaixo, determine seu centro de massa. Os corpos têm 3 kg, 5 kg e 8 kg de massa, e seus centros de gravidade individuais estão situados, respectivamente, nos pontos: (1, 6), (3, 2), (5,6).
![]()
Centro de massa em figuras planas homogêneas
Nas figuras geométricas regulares, o centro de massa coincide com o centro geométrico (centroide), no encontro dos eixos de simetria. Assim, conhecendo-se as dimensões da figura é possível calcular o centro de massa.
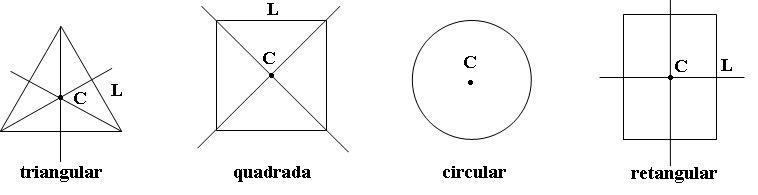
Nas figuras não regulares (e regulares também), o centro de gravidade pode ser determinado experimentalmente ou por cálculo.
No método experimental, basta que o corpo seja pendurado pela borda, por, pelo menos, dois pontos diferentes, um de cada vez. Cada ponto marcará o início de uma linha vertical, descendente. O encontro dessas linhas se dá exatamente no centro de massa.
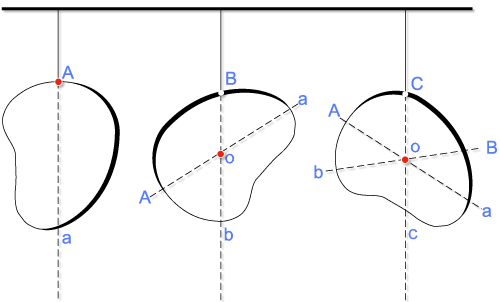
Clique aqui para fazer alguns testes desse tipo virtualmente.
É possível também calcular o centro de massa de uma figura qualquer. Por exemplo, seja a placa abaixo, com uma certa densidade superficial (kg/m2), e que pode ser dividida em dois retângulos, cujos centros de massa são os pontos (1,5, 2,5) e (4, 2).
O centro de massa da figura completa será dado pela média ponderada dos centros de massa de cada retângulo, onde o fator de ponderação será a massa de cada parte da figura. Supondo uma figura regular plana, de espessura constante e área “a", lembramos que ela terá uma densidade superficial (kg/m2) que será dada por:
Assim, substituindo na fórmula geral das coordenadas do centro de massa, faremos:
Observe que, como a densidade é constante, no caso de placas planas de densidade homogênea, o valor da densidade superficial não afeta o resultado, e apenas a área de cada figura componente pode ser usada para o cálculo.
Exercícios
Calcule o centro de massa das figuras planas abaixo (indicado pelo ponto azul e branco), usando como origem dos eixos o canto inferior esquerdo do quadro de cortiça:
Exemplo:
1. Separar a figura em partes simétricas, com o CG conhecido (pontos vermelhos).
2. Aplicar a fórmula acima
Link para o aplicativo acima:http://www.simbucket.com/combuilder/
Exercícios adicionais de centro de massa
Condição de Equilíbrio
Quando os corpos estão apoiados numa base, vale a seguinte condição:
Para que um corpo fique em equilíbrio, a condição necessária é que a linha de seu centro de massa não saia da base do corpo.
São três os tipos de equilíbrio em que um corpo pode estar:
Equilíbrio estável, onde o corpo volta para sua posição inicial se deslocado. Esta situação ocorre quando o ponto de sustentação está acima do centro de gravidade.
Equilíbrio instável, no qual o corpo se afasta de sua posição inicial, se deslocado.
Equilíbrio indiferente, no qual o corpo permanece em sua nova posição, se deslocado.
Exemplos
Numa edificação com apoio simples, como ilustrado ao lado, se o centro de gravidade ultrapassar a base de apoio, a parede entrará em colapso.

Um veículo, por exemplo, não se manterá estável se a linha do centro de gravidade ultrapassar o pneu.
Quando mais alto o centro de gravidade do veículo, maior deverá ser a distância entre as rodas.
Isso deve ser levado em conta também na distribuição das cargas em um caminhão. Cargas altas ou concentradas em um dos lados do caminhão favorecem o capotamento.
No caso de um içamento, a condição de equilíbrio é que o ponto pelo qual a carga é levantada deve estar acima do centro de massa da carga. Nessa situação, se houver um desequilíbrio, a carga retornará ao ponto de equilíbrio (equilíbrio estável).
Caso o ponto de içamento se localizar abaixo do centro de gravidade, a carga estará em equilíbrio instável, e irá tombar ao menor afastamento do ponto de equilíbrio (equilíbrio instável).
No caso de um navio, o ponto de aplicação da força de empuxo (a força que faz o navio flutuar) chama-se centro de empuxo (CE). O centro de empuxo localiza-se no centro de gravidade da sessão da água que o navio desloca.
Para que a embarcação fique em equilíbrio estável, o centro de empuxo deve estar acima do centro de massa da embarcação.
Fonte: A Física nas embarcações
Obs: sobre a Lei do Empuxo, acesse aqui.
Exercício
As três figuras abaixo estão nas suas posições de inclinação máxima antes do tombamento. Calcule o ângulo de inclinação de cada uma delas em relação ao eixo vertical e explique a diferença.
Condição de equilíbrio em alavancas
No caso particular do equilíbrio de corpos independentes, numa alavanca balanceada, por exemplo, a condição de equilíbrio estável ocorrerá quando o ponto de apoio coincidir com o centro de gravidade do conjunto. Em outras palavras, será aquele em que todas as massas envolvidas produzirem o mesmo torque em relação ao ponto de apoio.
Por exemplo, seja uma alavanca com a distribuição de cargas ilustrada abaixo. Este sistema está em equilíbrio, pois o ponto de apoio coincide com o centro de gravidade do conjunto das duas massas, como demonstrado a seguir.
Como a distribuição, neste caso, se dá apenas no eixo x, apenas esse será considerado. Estabelecendo arbitrariamente a origem do eixo x na primeira marca da esquerda da alavanca, teremos:
O sistema está, então, em equilíbrio, pois o ponto de apoio da alavanca está exatamente alinhado com o centro de gravidade calculado acima (x=4).
Para que a condição de equilíbrio ocorra, portanto, se assumirmos que o ponto de apoio estará na origem das distâncias, deveremos ter sempre:
No exemplo acima, ficaria:
Como consequência, podemos dizer que, para que a alavanca esteja em equilíbrio, o módulo do produto das massas que produzem torque em um sentido, deve ser igual ao produto das massas que produzem torque no outro:
Exemplo
Na distribuição em equilíbrio abaixo, qual o valor da massa F?
Exercícios
Nas situações abaixo, calcule o valor da massa faltante para que a alavanca esteja em equilíbrio:
Links interessantes
Um atleta faz uso da Física para quebrar recordes mundiais - Asaf Bar-Yosef - YouTube
MIT Physics Demo -- Center of Mass Trajectory - YouTube
Material da aula
Slides da aula (inclui vigas biapoiadas)