Energia
Trabalho e energia são grandezas muito relacionadas. Vimos que o trabalho representa a diferença de dois estados energéticos de um sistema. Por sua vez, a energia pode ser definida como a capacidade de realizar trabalho. Quer dizer que, se temos um sistema com um certo nível de energia, ele pode realizar trabalho e seu nível de energia diminuirá na mesma quantidade do trabalho realizado. O trabalho será a diferença entre os estados de energia inicial e final. É o que acontece, por exemplo, quando a água de uma usina hidroelétrica, na sua queda, aciona uma turbina geradora.
No contexto da Física Mecânica, consideraremos 3 tipos de energia:
- A energia cinética, associada ao movimento de um corpo
- A energia potencial, associada à altura de um corpo
- A energia elástica, associada ao grau de deformação de uma mola
Energia cinética
Quando aplicamos uma força sobre um corpo produzimos neste um movimento acelerado, que pode ser descrito pela equação da velocidade de Torricelli:
Isolando a aceleração, teremos:
Como, pela segunda lei de Newton temos que:
Podemos fazer o seguinte desenvolvimento:
Conforme vimos, da definição de trabalho temos que:
Assim, podemos fazer:
Chamamos de Energia Cinética às grandezas definidas por:
e
__________
Sua unidade também é o Joule, pois:
Da segunda lei de Newton, temos que:
Substituindo, vem:
__________
Exemplos:
Um móvel de 5 kg está a uma velocidade constante de 10 m/s. Aplica-se uma força que eleva essa velocidade para 15 m/s. Calcular a energia cinética do móvel no estado inicial e final, e o trabalho aplicado.
Um carrinho de 2 kg desliza a uma velocidade constante de 3 m/s sobre uma superfície lisa de atrito desprezível, e entra numa superfície rugosa, parando em 18 cm. Qual foi a força de atrito que atuou para fazer o carrinho parar?
Como comparação, esse problema poderia ser resolvido com as fórmulas da Cinemática e Dinâmica.
Exercícios propostos
Um veículo de 1200 kg parte do repouso e após 10 s atinge 100 km/h. Qual foi o trabalho realizado nesse intervalo? Com que potência em CV? (1 CV=735 W) Resposta:4,64x105 J, 63 CV. Resolução
Qual a força necessária para parar uma carreta de 50 T que está a 50 km/h numa distância de 200 m? Resposta: 2,38x104N. Resolução
Uma flecha de 264 g atinge uma placa de madeira com uma velocidade de 60 m/s penetrando 2 cm. Calcule a força que a placa exerceu sobre a flecha. Resposta:2,38x104N. Resolução
Energia Potencial
Um corpo pode estar parado, mas ter potencial para entrar em movimento. Por exemplo, a água de uma represa, ou um corpo sujeito à ação de uma mola.
Chamamos esses dois tipos de energia potencial de energia potencial gravitacional e energia potencial elástica. As forças responsáveis for elas são, respectivamente, a força da gravidade e a força elástica. Elas são chamadas de forças conservativas. Por exemplo, quando elevamos uma pedra, toda a energia gasta para elevá-la fica ‘conservada’ nela. A força elástica também é uma força conservativa. Uma força pode ser dissipativa também, como o atrito.
A energia potencial gravitacional de um corpo corresponde ao trabalho gasto em aumentar sua altura.
A energia potencial elástica de uma mola corresponde ao trabalho realizado para comprimi-la:
Conservação da energia
Um dos princípios mais importantes da Física é o da conservação de energia. Já há muito se observa que a quantidade total de energia de um sistema permanece constante. Assim, a energia potencial mecânica acumulada nas águas de uma represa se transformam em energia elétrica, nos geradores, mais as perdas por atrito, calor, etc. A energia potencial de um pêndulo se transforma em energia cinética à medida em que ele se aproxima do ponto mais baixo.

Numa queima de fogos de artifício, a energia química é transformada em energia térmica, luminosa e cinética.
Considerando as formas de energia mecânica, segundo esse princípio, na ausência de forças dissipativas (como o atrito), é correto afirmar que toda a energia cinética se transforma em energia potencial e vice-versa, de modo que a energia mecânica total de um sistema permanece constante. Ou seja:
Na animação abaixo a energia cinética é representada por K, a energia potencial elástica por U e a energia mecânica total por E. Repare que quando a energia potencial elástica é máxima, a energia cinética é nula, isto é, o corpo está temporariamente parado. A velocidade máxima, e portanto a energia cinética máxima, é atingida no momento a mola está na posição de repouso, ou seja, quando a energia potencial elástica é nula. Porém, a soma das duas permanece constante.
Com base nesse princípio é possível encontrarmos a solução de vários problemas na Mecânica.
Exemplos
1. Uma maçã de 300 g desprende-se do galho a 3 metros de altura. Com que velocidade chegará ao solo?
Solução: as formas de energia do problema são cinética e potencial.
No problema acima é possível observar que a massa não influi no resultado.
2. Um corpo com massa 5 kg está apoiado numa superfície e comprime uma mola de constante elástica k=500 N/m. A deformação da mola é de 40 cm. Determine a velocidade que ele alcança ao ser liberado e perder o contato com a mola.
Solução: as formas de energia do problema são elástica e cinética.
A energia cinética inicial é zero, já que a velocidade é zero, e a energia potencial elástica final é zero. Assim, teremos:
3. Determinar a altura mínima h em que o carrinho da figura deve ser abandonado para que ele consiga realizar o loop, considerando que o raio R é de 2 metros e que o atrito é desprezível.
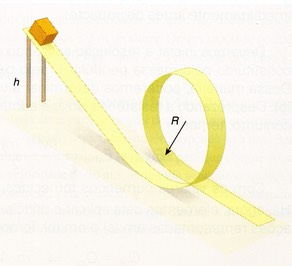
Primeiro é necessário calcular a velocidade mínima no ponto mais alto do loop. Nesse ponto, o módulo da força peso deverá ser igual ao módulo da força centrípeta.
Portanto:
Para garantir que essa velocidade seja alcançada, a quantidade de energia no ponto do abandono deve ser igual à energia nesse ponto. No início da rampa existe apenas energia potencial, já que a velocidade é zero. No alto do loop, temos energia cinética e energia potencial:
Assim a altura mínima deve ser de 5 metros. Repare que a massa não altera o resultado.
Exercícios propostos:
4. Um carrinho percorre sem atrito a pista esquematizada abaixo. Calcule qual deve ser a velocidade escalar mínima em A para que o carrinho alcance o ponto C e qual o valor da velocidade em C.
Resposta: 6,26 m/s. Resolução
5. Determinar a constante elástica de uma mola que garanta que um carrinho de massa 3 kg atinja uma rampa a altura de 5 metros com uma velocidade de 2 m/s, conforme o desenho, sendo deformada de 50 cm.
Resposta: 1226 N/m. Resolução
6. Uma mola com constante elástica de 150 N/m, comprimida de 25 cm, é liberada e empurra uma esfera de 500 g no ponto A pela trajetória representada. Calcule (a) a velocidade da esfera assim que é liberada pela mola, (b) com que velocidade ela passará pelo ponto B, que fica 30 cm acima de A e (c) qual seria a maior altura em que a rampa B poderia ser colocada (na qual a velocidade da esfera seria nula).
Resposta: (a) 4,33 m/s; (b) 3,59 m/s; (c) 95,6 cm. Resolução
Slides usados na aula
Exercícios
Lista de exercícios de cálculo (pdf) - Fonte: NICOLAU, G. F. et al. Física: ciência e tecnologia. São Paulo: Moderna, 2001
Exercícios de alternativas (site Física e Vestibular)
Simulador
Fonte: PhET - University of Colorado